‌

Expressions Structure

Heads

For any expression the part before the square brackets is known as the Head of the expression and happily there is the conveniently named Head function extract it!

 Head@<|1->2, 3->4, 5->6|>

 Association

The Head of an expression can be anything. It can be a string:

 Head@"a"[b]

 "a"

A compound expression:

 Head@((12 s^2)[2])

 12 s^2

Or a deeply-nested chain of expressions:

 Head@(f[1][<|a->b|>][3])

 f[1][<|a->b|>]

Parts

Everything following the Head in the expression is simply a part of the expression and can be extracted with the Part function.

Here the part 1 is the part within the brackets:

 Part[((12s^2)[2]), 1]

 2

And here part 2 second bit in the curly bracesL

 Part[{1,2,3}, 2]

 2

But if we look at the FullForm of that:

 {1,2,3}//FullForm

 List[1,2,3]

We see that it's really no different than the first example

Part also has an alias [[ ]]

 {1,2,3}[[2]]

 2

It can also take runs of elements using Span syntax:

 Range[10][[2;;8;;3]]

 {2,5,8}

Or it can take a list of elements:

 Range[100, 1, -1][[Array[Fibonacci, 10]]]

 {100,100,99,98,96,93,88,80,67,46}

Because so often one needs the first or last components of an expression there are two dedicated functions to getting these parts.

First is functionally equivalent to [[1]] :

 First@Range[10]

 1

And Last is functionally equivalent to [[-1]] :

 Last@Range[10]

 10

There is also the function Rest which will take the second through last parts of an expression:

 Rest@A[1, 2, 3, 4, 5]

 A[2,3,4,5]

And Most which will that the first through second to last parts:

 Most@A[1, 2, 3, 4, 5]

 A[1,2,3,4]

There is also the function Take which takes spans from an expression:

 Take[B@@Range[10],{3,5}]

 B[3,4,5]

Take also accepts Span syntax

There is also Extract which is much like Part but provides a few features that can make it much more efficient in some cases (and less efficient in others). If you're going to do a lot of numeric manipulation or manipulation of memory-hungry objects it's worth being comfortable with both.

Manipulating Expressions

Mathematica also supports the manipulation of expressions through a wide series of functions, a few of which will be explained here and more which will be explained later:

Insert takes an expression and inserts another expression in the index specified as its third argument

 Insert[{1,2,4}, "Hi", -1]

 {1,2,4,"Hi"}

As expected, it can insert into an arbitrary expression:

 Insert[A[1,2,4], "Hi", -2]

 A[1,2,"Hi",4]

We can use this to, for example, insert another Sphere into a Graphics3D expression:

 Graphics3D[{Sphere[]},ImageSize->Small]//Insert[#, Sphere[{2,2,2}, .5], {1,-1}]&

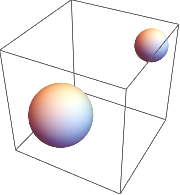
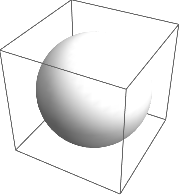
Append and Prepend take an expression and add an element at the end and beginning respectively

 Append[Graphics3D[Sphere[],ImageSize->Small], Lighting->"Neutral"]

Delete and Drop both remove parts from an expression. Delete drops a single part:

 Delete[A[1,2,3,4,5],4]

 A[1,2,3,5]

Drop removes a span of parts

 Drop[A[1,2,3,4,5],-2]

 A[1,2,3]

Sequence

Often one wants to do something like stick the arguments of one expression inside another one. For this purpose there is a special HeadSequence

 A[1,2,3,Sequence[1,2,3]]

 A[1,2,3,1,2,3]

Or demonstrating how to put a list inside the expression:

 A[1,2,3,Sequence@@{1,2,3}]

 A[1,2,3,1,2,3]

Sequence generally represents a sequence of arguments which will be used without a Head . It is used most often in pattern matching and function definitions, but, being such a flexible construct, it has many uses.