‌

Hold⋆ and Evaluation Order

We’ve touched on evaluation order briefly when we introduced UpValues but there are a series of other things to consider. For example say you want to define a function that makes a string of print commands to display. Naively we might try the following:

 Column@(ToString /@ {Print[1], Print[2], Print[3]})

But Print evaluates before ToString so we’ll need to format a different way. We can try it with Hold

 Column@(ToString /@ Hold[Print[1], Print[2], Print[3]])

 Column[Hold[ToString[Print[1]], ToString[Print[2]], 
  ToString[Print[3]]]]

Hold prevents the evaluation of the command it’s wrapped around. Unfortunately that applies to ToString too.

Our solution is instead to use Unevaluated

 Column@(ToString /@ {Unevaluated@Print[1], Unevaluated@Print[2], 
    Unevaluated@Print[3]})

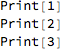
Unevaluated has no meaning on it’s own, but when wrapped around an expression essentially says to use that expression it is Unevaluated form.

Its counterpart is Evaluate , which forces the evaluation of a held expression:

Hold[Evaluate@∫0πSin[θ]ⅆθ]

 Hold[2]

Note that Evaluate only works when on the first level of the expression though:

Hold[1 + Evaluate@∫0πSin[θ]ⅆθ]

Hold[1 + Evaluate[∫0πSin[θ]ⅆθ]]

Hold is often used with Thread to create lists of held expressions:

Column@Thread@Hold[{
    ∫2πSin[θ]ⅆθ,
    ∫1πSin[θ]ⅆθ,
    ∫0πSin[θ]ⅆθ}]

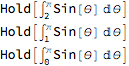
It’s also used with the Replace function family to manipulate expressions without evaluation:

Hold[a[1], b[], c[1]] /. {
  a -> Print,
  _b :> ∫2πSin[θ]ⅆθ,
  c -> CreateDocument}

Hold[Print[1], ∫2πSin[θ]ⅆθ, CreateDocument[1]]

Note that Print[2] is inserted into the Hold without evaluation.

There’s a trick to getting it do evaluate:

Hold[a[1], b[], c[1]] /. {
  a -> Print,
  _b :> With[{r = ∫2πSin[θ]ⅆθ}, r /; True],
  c -> CreateDocument}

 Hold[Print[1], 1 + Cos[2], CreateDocument[1]]

Why this works will be explained later, for now just keep in mind as a useful trick